
先に作成した数独(ナンバープレイス)解法プログラムは9x9サイズの問題を解くことが出来るが専門誌に掲載されている9x9サイズ以外の問題を解くことが出来ない。
専門誌にはブロックサイズが4x4の16x16サイズや5x5の25x25サイズの問題とかが掲載されている。それらの問題に対し虱潰し法でアプローチすると計算量が膨大になりすぎて実用的な速度で応答を得ることが出来ない。そこでそれらの問題に対しては,ヒューリスティックな方法でアプローチすることにした。要するに人間がやっていることと同じことをプログラムでやってしまおうと言うこと。
専門誌ではナンプレと表記しているものが殆どなので,以降数独(ナンバープレイス,ナンバープレース)はナンプレと表記する。ナンプレ雑誌は結構出版されているんだねー。
ここでは9x9サイズ以外にも対応したプログラムに関する解説をする。作成したプログラムは雑誌に掲載されているナンプレ問題を解ける程度の性能を有する(ナンプレで最大のサイズのものはどれ位の大きさなんだろう?)。
2009.05.04
お待たせしました。ソースを見たい人はこちらをダウンロードしてください。開発言語はC++です。Algol(アルゴル)系の言語がわかる人なら見れば判ると思いますが,そうでない人はお手上げです。
候補値は高速化のためビットで表現しています。
sudoku.cpp内のMAX64を1に設定すれば64x64の大きさの問題まで解くことが出来ます。ビット方式で作成したので通常は4バイトで表現できる32x32の大きさが最大です。
ノーマルの他,クラッシックナンプレ,対角ナンプレ,幾何学ナンプレ,カラーナンプレ,不等号ナンプレ,一つ違いナンプレ,0to9ナンプレ,頭でっかちナンプレ,重ね合わせナンプレ(合体ナンプレ)に対応しています(それぞれクラスを作成)。
sudoku.cpp以外はデバッグ出力が残っているので,気になる人はps()を見かけたら削除してください。
2009.05.07
WIN32のDev6(CompilerはVersion12)で開発しましたがUNIXでも動作するように修正しました。gcc -lstdc++ SudokuReader.cpp
でコンパイルできます。
プログラムの肝となる部分は以下の通り。
while( 数字が確定した) {
確定できる数字を探す。
ルールを適用し,可能性のある数字を減らす。
}
実際には確定出来る数字を探す部分が一回の操作では確定できない場合があり,候補となる数字を削除するだけになることがあるので,プログラムを継続する条件を以下のようにする。
while( 数字を確定した || 候補数字を減らすことが出来た) {
確定できる数字を探す。
ルールを適用し,可能性のある数字を減らす。
}
肝となる部分はこれだけである。
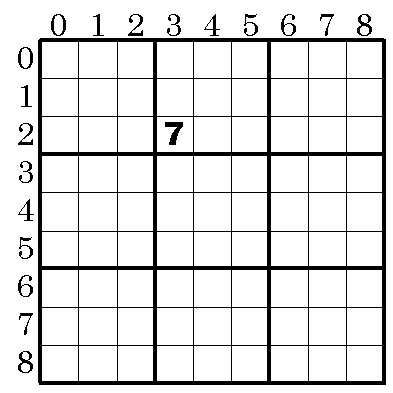
問題図を以下のような0オリジンの二次元配列であると見なす。ブロック(内部の太線で囲まれた領域)の大きさをrows, cols とする。配列は正方形で,一辺の長さMはrows*colsである。

配列は [行][列] でアクセスする。例えば,以下の図の7(2行3列にある)は位置 [2][3] である。
可能性のある数字をビット位置で表現し以下のように定義しても良いのだが,
ulong mat[M][M];
プログラムの判り易さを考え,可能性のある数字を0オリジンの3次元配列で定義する。値が1の場合可能性あり,0の場合可能性無しと見なす。
(結局2009年にプログラムを一から作り直した時にビット方式にしてしまった。)
byte mat[M][M][M+1];
普通のナンプレの場合9x9(3x3のブロック)であるので,Mは9になる。rows=3, cols=3 である。
[1][5]で可能性のある数字が2,3,8,9であるとしたら,ビット方式では
mat[1][5] = 0x186; // 110000110
となる(数字1を1ビット目から始めた場合)。3次元方式だと以下のようになる。
mat[1][5][0] = 0; // [0]は使用しない mat[1][5][1] = 0; mat[1][5][2] = 1; // 可能性あり mat[1][5][3] = 1; // 可能性あり mat[1][5][4] = 0; mat[1][5][5] = 0; mat[1][5][6] = 0; mat[1][5][7] = 0; mat[1][5][8] = 1; // 可能性あり mat[1][5][9] = 1; // 可能性あり
以下の条件の何れかを満たせば数字を確定することが出来る。
以下の問題を例に解説する。
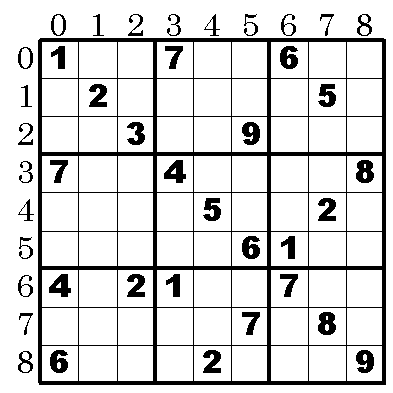
上記問題で2の候補数字を削除すると,以下の白マスしか2を置くことが出来ないことが判る。以下の状態で,[5][0]には2が入ることが判る。何故ならこの位置のブロックには白マスが一つしか残っていないから。
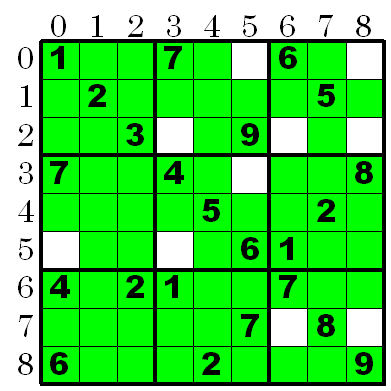
この方法で候補数字が1つしか無いものを順に確定していくと以下のようになる。
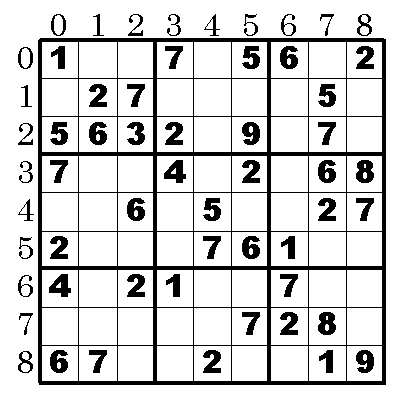
上記図で[6][7]に注目する。
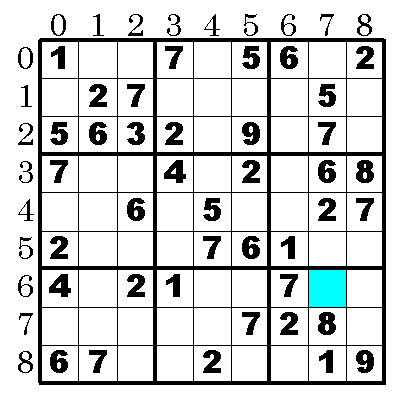
ぱっと見た目,この位置に置ける数字は3,4,5,6の4つしか残っていないことが判る(このブロックでは1,2,7,8,9が既に確定しているので)。しかし,以下の図のように4,5,6は候補値として認められないことが判る。すると[6][7]の候補値として残るのは3だけになる。
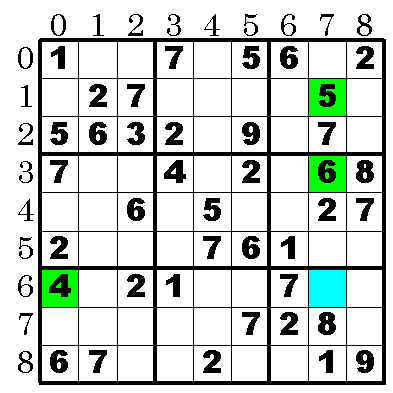
よって[6][7]の数字は3に確定する。
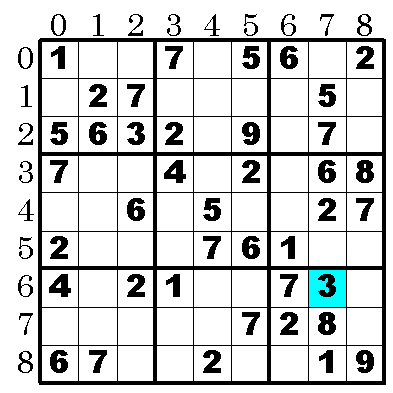
数字を確定できるルールは上記2つのみである。
上記をプログラムすると以下のようになる。
for( col=0; col< M; col++) {
mat[row][col][k] = 0;
}
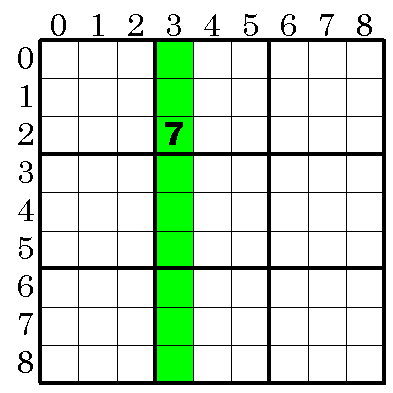
以下の図で7が確定すると緑色の部分は7の可能性が無くなる。
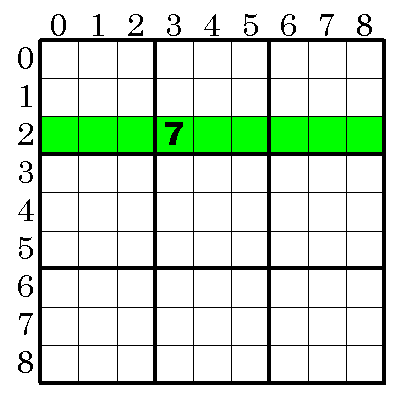
for( row=0; row< M; row++) {
mat[row][col][k] = 0;
}
以下の図で7が確定すると緑色の部分は7の可能性が無くなる。
for( row=0; row< rows; row++) {
for( col=0; col< cols; col++) {
mat[rowBlockFirst+row][colBlockFirst+col][k] = 0;
}
}
以下の図で7が確定すると緑色の部分は7の可能性が無くなる。
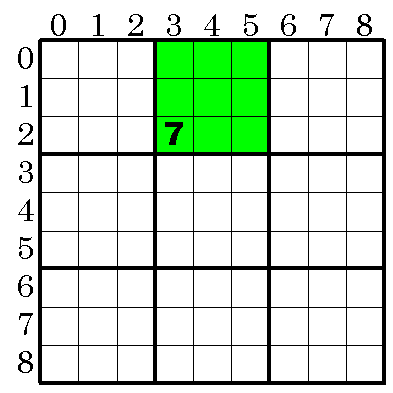
ある位置[row][col]で数字が確定した場合の処理を既に述べたが,それだけでは可能性除去には不足している(それだけで解ける簡単な問題もある)。
以下に,より強い可能性除去ルールに関して述べる。
ある数字(例えば7)だけを取り出して注目した場合,7を配置できる可能性が以下の図の通りであったとする。
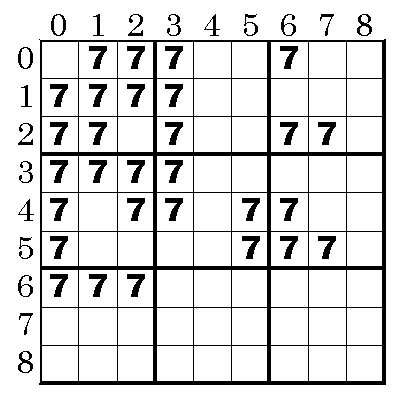
このとき以下の白抜きの7は可能性が無くなることが判る。何故なら[0][3],[1][3],[2][3]の何れかに7が入るので,[*][3]には7が入らないことが判る。
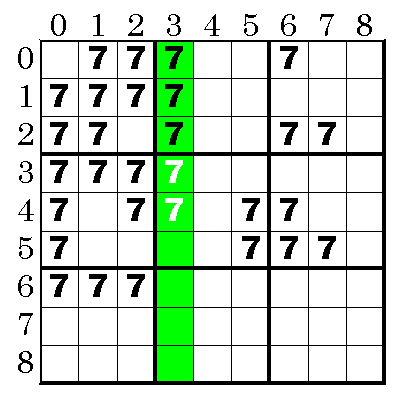
行,列の残りが特定ブロック内のみに存在するなら,そのブロック内の他の位置にある数字は可能性が無くなる。
例えば以下の図で行5の6は[5][6]か[5][8]にしか可能性が無くなったことが判る。そうすると,[3][8],[4][6],[4][8]の6は可能性を排除できる。

MATRIX内の可能性のある数字が以下のようになったとする。例えば,[2][0]は3,5,7,9の可能性がある。

このとき以下のブロック(紫部分)に注目する。

これをジーッと見ると,5と9が2箇所で使われているのが判る。

[2][0]で候補値3を選択すると,[2][0]の候補値5と9は削除されて,以下のようになる。

こうなると[2][1]の値として,5を選択すると9の置き場所が無くなり,9を選択すると5の置き場所が無くなることが判る。つまり,[2][0]に3を選択することが出来ないのである。
よって以下のように,[2][0]の3,7と[2][1]の6,7を候補値から除外できることが判る。

これをブロックだけでなく,行,列についても調べる。
「2個の数字が2升で使われている」でなく,より汎用化して「N個の数字がN升で使われている」場合を調べる。
これを効率的に調べる方法が判らないので,虱潰す。
今まで述べた方法で解けない問題も雑誌に掲載される場合がある。そのような場合可能性のある数字を虱潰すしか無いのだが,闇雲に虱潰そうとすると,計算量が膨大になる可能性がある。
そこで虱潰すにしてもなるべく計算量が少なくなるようにしたい。
候補値の少ないものから虱潰せば良いのだが,16x16の問題などでは,候補値が2個のマスが10個以上残ってしまうものがある。
候補値が少なく,なおかつ,そのマスが存在するブロック全体の候補値が少ないものを選んで虱潰すことにする。
残っている候補値が一番少ないブロックを探し,その中で更に候補値の少ないマスを探す。
色々なサイトで色々な手筋が公表されてますが,プログラムで解くには上記解法で十分です(実用上十分な速度で解答が得られる)。
9x9のナンプレの場合,1〜9までの数しか出現しなかったので,以下のように1マスの数字を1文字に割り当てることが出来た。
1..7..6.. .2.....5. ..3..9... 7..4....8 ....5..2. .....61.. 4.21..7.. .....7.8. 6...2...9
この形式はテンキーでの入力が容易であり,問題を入力するのが苦にならない。1文字を入力されたら1マスの値を確定することが出来るのでプログラムは簡便になる。
ところがサイズを拡張し10以上の数が出現すると,単純に1マスを1文字に割り当てることが出来なくなった。そこで1マスに2文字を割り当て数字は全て2桁で入力すると,入力が面倒であることが判る。
出来れば問題に書いてある数字をそのまま入力したい。例えば25x25サイズの場合25までの数を入力することが出来る。その時,曖昧になるのは1と2である。3〜9は必ず1桁の数字であることが判る。
1と2の場合,1なのか,後ろに来る数字と合わせて2桁の数字であるかが曖昧になるので,1桁の1を入力する場合は01,2を入力する場合は02を入力して貰い,それ以外は2桁と解釈するようにする。
これを一般的な考え方に拡張し,0は1桁数字のプレフィックスと見なす。そうするとテンキーだけで高速に入力することが出来る。