
朝日新聞土曜日の朝刊BeのEntertainment編に出題される(Beパズル)。毎週出題されると言う訳ではない。最初手で解いたのだが,3回やったら自動化したくなるため自動化する事を考えた。
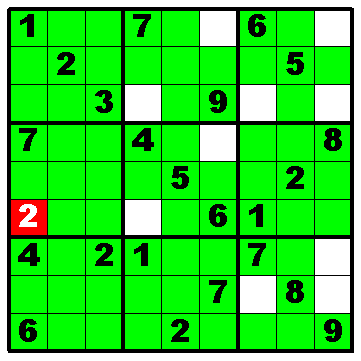
問題は例えば以下のような感じの図になる。

問題解法のためのルールは以下の通り。
このルールに沿って図を眺めると,例えば2は以下の白マスにしか置けないことが判る。

すると,ブロック内に白マスが1つしかない部分の2が確定し,そこが確定すると他の白マスの2も順に確定していくことが判る。
最初このような考えをプログラムに変換していったのだが,バックトラックを利用しなければならない問題があることに気づいた。9x9の数独の場合バックトラックのアルゴリズムを組み込んで,ヒューリスティックな部分を無効にしてもそれほど遅くなるものではないことに気づいた。つまり全編バックトラック法である。
結局虱潰しでプログラムすることにし,ヒューリスティックな部分を削除した。
虱潰しの利点は
プログラムがシンプルでバグ混入の恐れが無い。
逆に虱潰しの欠点は
下手をするとめちゃくちゃ実行時間が掛かる。
虱潰しでそこそこの実行速度が得られるのであれば,何も無理してヒューリスティックなアルゴリズムをプログラムに組み込む必要はないだろう。
9x9程度の数独の場合虱潰しても実用的な速度で解を得ることが出来る。世の中には数独雑誌が出版されている。それらの雑誌には16x16や大きいのになると28x28(ブロックは4x7)のサイズのものがあるが,それらの問題では虱潰し方法は時間が掛かりすぎてダメである。ヒューリスティックに解くプログラムを別に作成したので,そのアルゴリズムとソースはこちらを参照。
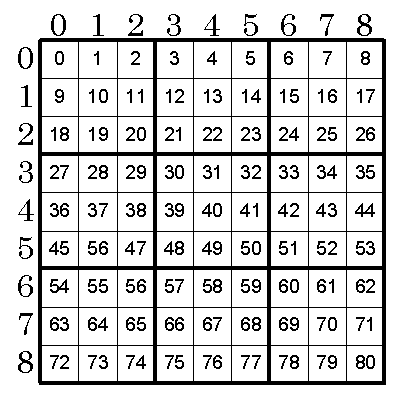
問題図を二次元の配列と見なし,以下のように番号を振る。マス数は9x9=81ある。
解を求める関数は以下のようになる。調査位置は行,列位置を1次元で表現した上記位置である。
Find( 調査位置)
{
if( 全てのマスに数字を設定した? ) {解が見つかった}
if( 調査位置に既に数字が置かれている?) {
Find( ++調査位置); // 出題時点で既に置かれている
}
else {
for( int i=1; i<= 9; i++) { // 1〜9の数字を置いてみる
mat[調査位置] = i; // この位置に数字iを置いてみる
if( 調査位置にiを置けるか?) { // 置くことによって矛盾が生じないか調べる
Find( ++調査位置); // 置けたら次の調査位置を調べる
}
mat[調査位置] = 0; // 仮定を取り消す
}
}
}
全てに数字を設定したかどうかは調査位置が81(=9x9)を超えたかどうかで解かる。Find()関数の調査位置は一次元で表現した方が簡単だが,問題図自体は二次元で表現した方が判りやすい。そこで実際には以下のように調査位置を行,列に変換して利用する。
row = 調査位置 / 9; col = 調査位置 % 9; mat[row][col]
最初の呼び出しは Find(0) とする。
ソースファイルはこちら。見直してみたら結構汚いソースファイルだったので,少し綺麗に書き換えた。
数字の決まっていない箇所をピリオド(.), 決まっている箇所を数字で9行記述する。
1..7..6.. .2.....5. ..3..9... 7..4....8 ....5..2. .....61.. 4.21..7.. .....7.8. 6...2...9
引数に問題図を入力したデータファイルを指定する。
9x9 data-file
欲しい人がいるかどうか判らないが,一応EXEファイルをダウンロードできるようにしておく。実行してみたい人はこちらをクリックしてダウンロードしてコマンドプロンプトを開いて実行してみてください。
プログラムを実行すると読み込んだ問題と結果を出力する。全ての場合を虱潰しているので,複数解存在する場合見つかっただけ出力する。
1..7..6.. .2.....5. ..3..9... 7..4....8 ....5..2. .....61.. 4.21..7.. .....7.8. 6...2...9 見つけた 184735692 927684351 563219874 731492568 846351927 259876143 492168735 315947286 678523419
ここに書いたプログラムは虱潰しの方法だが,この方法はサイズが大きくなると破綻する。
そこでちゃんとしたプログラムをどうやって作ったら良いか知りたい人はこちらのプログラムを参照してください。