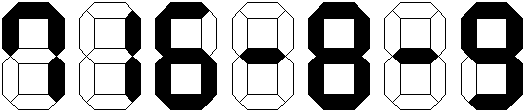
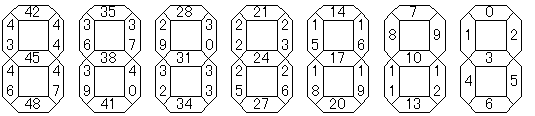
デジタル表示された以下の計算式がある。このうち2本の黒い棒を別の箇所に移して計算結果が最小の正の整数になるようにするには。
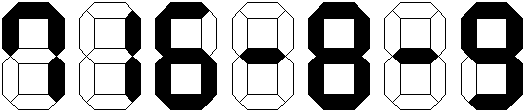
上記以外の数字の表示は以下の通り。
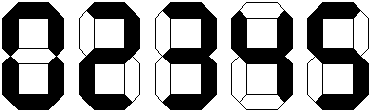
一番左の数字を0にするのはダメ。
いよいよ今回で最終回。最後を黒星で終えるのは嫌だったので,右下に解答が載っているけど見ないように努力してプログラムを作成。
棒とビット位置の割り当てを以下のようにする。
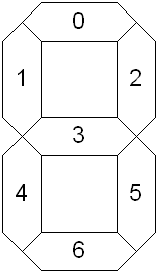
一つの数字を表現するのに7本の棒を使って合計7個の数字があるので,全部で棒は49本。49ビットで表現する。ビットの割り当ては以下の通り。
これを2箇所外して,別の2箇所に取り付けるので,虱潰しコードは以下のようになる。
A = 716-8-9 の棒の状態;
foreach( a in 49本の棒) {
B = A から 1本の棒aを除去
foreach( b in 49本の棒) {
C = B から 1本の棒bを除去
foreach( c in 49本の棒) {
D = C に 1本の棒cを追加
foreach( d in 49本の棒) {
E = D に 1本の棒dを追加
Eの計算が出来たら計算して,最小値を記録する
}
}
}
}
単純に考えると494(5,764,801)回のループになるけど実際は枝刈りが有効に機能してそれほどの回数でも無くなる。
これを実際のコードにすると以下のようになる。
int64 b49 =
makebit( i2b( 7),6)|
makebit( i2b( 1),5)|
makebit( i2b( 6),4)|
makebit( i2b(10),3)| // 10は'-'
makebit( i2b( 8),2)|
makebit( i2b(10),1)| // 10は'-'
makebit( i2b( 9),0);
A = b49;
for( int a=0; a< 49; a++) {
if( !(bit64(a) & A)) continue; // 使われていない棒を調べようとしている
B = A & ~bit64(a);
for( int b=0; b< 49; b++) {
if( !(bit64(b) & B)) continue; // 使われていない棒を調べようとしている
C = B & ~bit64(b);
for( int c=0; c< 49; c++) {
if( bit64(c) & C) continue; // 既にこの棒は使っている
D = C | bit64(c);
for( int d=0; d< 49; d++) {
if( bit64(d) & D) continue; // 既にこの棒は使っている
E = D | bit64(d);
int v = eval(E); // 計算式を評価する,負数は計算不可または最初の数が0
if( v > 0 && v < minv) { // 最小値を求める
minv= v;
ma = a, mb = b, mc = c, md = d;
mA = A, mB = B, mC = C, mD = D, mE = E;
}
}
}
}
}
利用している各関数は以下の通り。
const ulong bit0 = 0x00000001;
const ulong bit1 = 0x00000002;
const ulong bit2 = 0x00000004;
const ulong bit3 = 0x00000008;
const ulong bit4 = 0x00000010;
const ulong bit5 = 0x00000020;
const ulong bit6 = 0x00000040;
// bit 0 1 2 3 4 5 6 7 8 9 -
// .0. .0. ... .0. .0. ... .0. .0. .0. .0. .0. ...
// 1.2 1.2 ..2 ..2 ..2 1.2 1.. 1.. 1.2 1.2 1.2 ...
// .3. .3. ... .3. .3. .3. .3. .3. ... .3. .3. .3.
// 4.5 4.5 ..5 4.. ..5 ..5 ..5 4.5 ..5 4.5 ..5 ...
// .6. .6. ... .6. .6. ... .6. .6. ... .6. .6. ...
// 0 1 2 3 4 5 6 7 8 9 '-'
int _i2b[] = { 0x77, 0x24, 0x5d, 0x6d, 0x2e, 0x6b, 0x7b, 0x27, 0x7f, 0x6f, 0x08}; // 数字をビット表現に変換するためのテーブル
int _b2i[0x7F+10]; // ビット表現を数字に変換するためのテーブル(_i2b[]を逆に見る,main()で初期設定)
int i2b( int n) // 数字をビット表現に変換する
{
assert( n >= 0 && n <= 10); // n==10は'-'
return _i2b[n];
}
int b2i( int b) // ビット表現を数字に変換する
{
assert( (b&~0x7F) == 0);
return _b2i[b]; // _b2i[]は_i2b[]を使って初期化しておく必要がある
}
int64 makebit( int v, int shift) // 1個の数字が7ビット,それを49ビット中に7個入れることが出来る
{
int64 v64 = v;
assert( (v&~0x7F)==0);
v64 <<= (shift*7); // 1つの数字で7ビット
return v64;
}
int64 bit64( int p) // bit<p> を求める
{
int64 b = 1;
b <<= p;
return b;
}
int eval( int64 e) // 計算式を評価する
{
int v[7]; // 取り出した7個の数字を入れる予定
for( int i=0; i< 7; i++) { // 右から順に数字を取り出す
int val = e & 0x7F; // 7ビット取り出し
v[i] = b2i(val); // それを数値に変換する
if( v[i] < 0) return -1; // 変換できない数字が出現した
e >>= 7; // 次に取り出す数値
}
// v[0]〜v[6]に取り出した数字が入っている,v[0]が一番右の数字
int n = 0; // 数字の個数
int N[7] = {0}; // 出現数字
int sign = 1; // 出現数字の符号
if( v[6] == 0) return -1; // 先頭の数字が0の場合は題意に沿わない
for( i=0; i< 7; i++) {
int val = v[7-i-1]; // 左の数字から取り出す
if( val == 10) { // '-'が出現した
n++; // 以降,新しい数字と見なす
sign = -1; // 負数が出現したことになる
continue; // 次の数字を見に行く
}
N[n] *= 10; //
N[n] += val * sign; // 負数の場合も考慮して数字を評価する
}
int result = 0;
for( i=0; i<= n; i++) { // 計算する
result += N[i]; // 負数はマイナスでN[i]に入っているので足すだけで済む。
}
return result; // 計算結果
}
答えが無事出力されたので右下の解答と比較,合っていることを確認。最後を白星で飾れたのでひとまず満足。
出題者の方2年間お疲れ様でした。
私のように間違いを繰り返すわけにはいかないので大変だったろうと思う。
私は「趣味はプログラミングです」なので,これから寂しくなるなー。
ここは会社のホームページだけとトップページがいきなり「パズル横丁」だったからこれからどうしようかな。
解速度
即