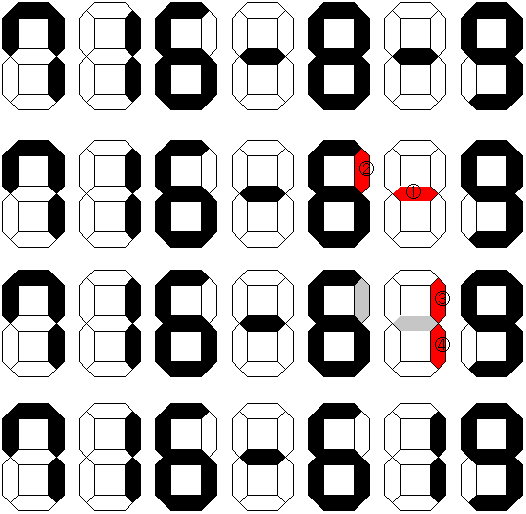
プログラム実行結果は以下の通り。
init: 7 1 6 -8 -9 = 699 remove .-.|.-.|.-.|.-.|.-.|.-.|.-.| -.-|-.-|-.-|-.-|-.-|-.-|-.-| .-.|.-.|.-.|.-.|.-.|.X.|.-.| -.-|-.-|-.-|-.-|-.-|-.-|-.-| .-.|.-.|.-.|.-.|.-.|.-.|.-.| remove .-.|.-.|.-.|.-.|.-.|.-.|.-.| -.-|-.-|-.-|-.-|-.X|-.-|-.-| .-.|.-.|.-.|.-.|.-.|.-.|.-.| -.-|-.-|-.-|-.-|-.-|-.-|-.-| .-.|.-.|.-.|.-.|.-.|.-.|.-.| add .-.|.-.|.-.|.-.|.-.|.-.|.-.| -.-|-.-|-.-|-.-|-.-|-.X|-.-| .-.|.-.|.-.|.-.|.-.|.-.|.-.| -.-|-.-|-.-|-.-|-.-|-.-|-.-| .-.|.-.|.-.|.-.|.-.|.-.|.-.| add .-.|.-.|.-.|.-.|.-.|.-.|.-.| -.-|-.-|-.-|-.-|-.-|-.-|-.-| .-.|.-.|.-.|.-.|.-.|.-.|.-.| -.-|-.-|-.-|-.-|-.-|-.X|-.-| .-.|.-.|.-.|.-.|.-.|.-.|.-.| result: 7 1 6 -6 1 9 = 97
これを図にすると以下のようになる。
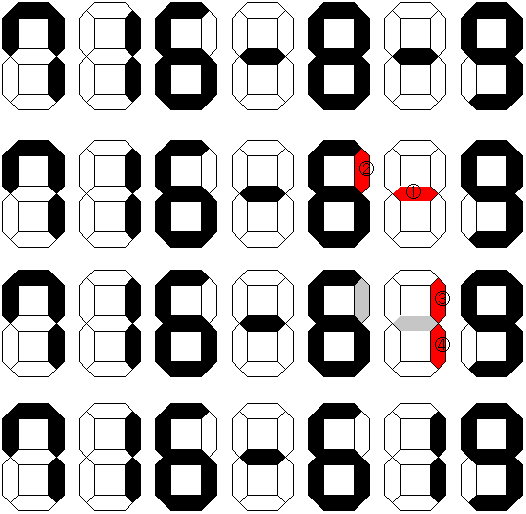
プログラムのソースは以下の通り。
#include "puzutl.h"
#include <math.h>
const ulong bit0 = 0x00000001;
const ulong bit1 = 0x00000002;
const ulong bit2 = 0x00000004;
const ulong bit3 = 0x00000008;
const ulong bit4 = 0x00000010;
const ulong bit5 = 0x00000020;
const ulong bit6 = 0x00000040;
// bit 0 1 2 3 4 5 6 7 8 9 -
// .0. .0. ... .0. .0. ... .0. .0. .0. .0. .0. ...
// 1.2 1.2 ..2 ..2 ..2 1.2 1.. 1.. 1.2 1.2 1.2 ...
// .3. .3. ... .3. .3. .3. .3. .3. ... .3. .3. .3.
// 4.5 4.5 ..5 4.. ..5 ..5 ..5 4.5 ..5 4.5 ..5 ...
// .6. .6. ... .6. .6. ... .6. .6. ... .6. .6. ...
// 0 1 2 3 4 5 6 7 8 9 '-'
int _i2b[] = { 0x77, 0x24, 0x5d, 0x6d, 0x2e, 0x6b, 0x7b, 0x27, 0x7f, 0x6f, 0x08}; // 数字をビット表現に変換するためのテーブル
int _b2i[0x7F+10]; // ビット表現を数字に変換するためのテーブル(_i2b[]を逆に見る,main()で初期設定)
int i2b( int n) // 数字をビット表現に変換する
{
assert( n >= 0 && n <= 10); // n==10は'-'
return _i2b[n];
}
int b2i( int b) // ビット表現を数字に変換する
{
assert( (b&~0x7F) == 0);
return _b2i[b]; // _b2i[]は_i2b[]を使って初期化しておく必要がある
}
int64 makebit( int v, int shift) // 1個の数字が7ビット,それを49ビット中に7個入れることが出来る
{
int64 v64 = v;
assert( (v&~0x7F)==0);
v64 <<= (shift*7); // 1つの数字で7ビット
return v64;
}
int64 bit64( int p) // bit<p> を求める
{
int64 b = 1;
b <<= p;
return b;
}
int eval( int64 e) // 計算式を評価する
{
int v[7]; // 取り出した7個の数字を入れる予定
for( int i=0; i< 7; i++) { // 右から順に数字を取り出す
int val = e & 0x7F; // 7ビット取り出し
v[i] = b2i(val); // それを数値に変換する
if( v[i] < 0) return -1; // 変換できない数字が出現した
e >>= 7; // 次に取り出す数値
}
// v[0]〜v[6]に取り出した数字が入っている,v[0]が一番右の数字
int n = 0; // 数字の個数
int N[7] = {0}; // 出現数字
int sign = 1; // 出現数字の符号
if( v[6] == 0) return -1; // 先頭の数字が0の場合は題意に沿わない
for( i=0; i< 7; i++) {
int val = v[7-i-1]; // 左の数字から取り出す
if( val == 10) { // '-'が出現した
n++; // 以降,新しい数字と見なす
sign = -1; // 負数が出現したことになる
continue; // 次の数字を見に行く
}
N[n] *= 10; //
N[n] += val * sign; // 負数の場合も考慮して数字を評価する
}
int result = 0;
for( i=0; i<= n; i++) { // 計算する
result += N[i]; // 負数はマイナスでN[i]に入っているので足すだけで済む。
}
return result; // 計算結果
}
void b2buf( char buf[7][5][3], int idx, int v)
{
for( int row=0; row< 5; row++) {
for( int col=0; col< 3; col++) {
buf[idx][row][col] = '.';
}
}
if( v & bit0) buf[idx][0][1] = 'X'; else buf[idx][0][1] = '-';
if( v & bit1) buf[idx][1][0] = 'X'; else buf[idx][1][0] = '-';
if( v & bit2) buf[idx][1][2] = 'X'; else buf[idx][1][2] = '-';
if( v & bit3) buf[idx][2][1] = 'X'; else buf[idx][2][1] = '-';
if( v & bit4) buf[idx][3][0] = 'X'; else buf[idx][3][0] = '-';
if( v & bit5) buf[idx][3][2] = 'X'; else buf[idx][3][2] = '-';
if( v & bit6) buf[idx][4][1] = 'X'; else buf[idx][4][1] = '-';
}
void dump( cstring msg, int v) // bitの立っている位置を'X'で出力する
{
char buf[7][5][3]; // buf[7個の数字][縦][横]
for( int i=0; i< 7; i++) {
b2buf( buf, 7-i-1, v&0x7F);
v >>= 7;
}
ps( "%s\n", msg);
// 以下のような出力をする。ちょっと判りづらいけど我慢。
// .-.|.-.|.-.|.-.|.-.|.-.|.-.|
// -.-|-.-|-.-|-.-|-.-|-.-|-.-|
// .-.|.-.|.-.|.-.|.-.|.-.|.-.|
// -.-|-.-|-.-|-.-|-.-|-.X|-.-|
// .-.|.-.|.-.|.-.|.-.|.-.|.-.|
for( int row=0; row< 5; row++) {
for( int idx=0; idx< 7; idx++) {
for( int col=0; col< 3; col++) {
ps( "%c", buf[idx][row][col]);
}
ps( "|");
}
ps( "\n");
}
ps( "\n");
}
void dump49( cstring msg, int64 v) // 式を評価して出力する
{
int R = eval(v);
int val[7];
for( int i=0; i< 7; i++) {
val[7-i-1] = v & 0x7F;
v >>= 7;
}
ps( "%s: ", msg);
for( i=0; i< 7; i++) {
int n = b2i(val[i]);
//if( n < 0) ps( "(%d,%d)", n, val[i]);
if( n == 10) ps( "-");
else ps( "%d ", n);
}
if( R > 0) ps( "= %d\n", R);
else ps( "= ERROR(%d)\n", R);
}
int main( int argc, cstring argv[])
{
for( int i=0; i< 0x7F+10; i++) {
_b2i[i] = -1;
}
for( i=0; i<= 10; i++) { // 0〜9と10=='-'
_b2i[_i2b[i]] = i;
}
int64 A, B, C, D, E;
int64 mA, mE;
int v, minv = 9999999, ma, mb, mc, md; // 最小値と取り出す棒
int64 b49 =
makebit( i2b( 7),6)|
makebit( i2b( 1),5)|
makebit( i2b( 6),4)|
makebit( i2b(10),3)| // 10は'-'
makebit( i2b( 8),2)|
makebit( i2b(10),1)| // 10は'-'
makebit( i2b( 9),0);
A = b49;
for( int a=0; a< 49; a++) {
if( !(bit64(a) & A)) continue; // 使われていない棒を調べようとしている
B = A & ~bit64(a);
for( int b=0; b< 49; b++) {
if( !(bit64(b) & B)) continue; // 使われていない棒を調べようとしている
C = B & ~bit64(b);
for( int c=0; c< 49; c++) {
if( bit64(c) & C) continue; // 既にこの棒は使っている
D = C | bit64(c);
for( int d=0; d< 49; d++) {
if( bit64(d) & D) continue; // 既にこの棒は使っている
E = D | bit64(d);
int v = eval(E); // 計算式を評価する,負数は計算不可または最初の数が0
if( v > 0 && v < minv) { // 最小値を求める
minv= v;
ma = a, mb = b, mc = c, md = d;
mA = A, mE = E;
}
}
}
}
}
dump49("init", mA);
dump("remove", bit64(ma));
dump("remove", bit64(mb));
dump("add", bit64(mc));
dump("add", bit64(md));
dump49("result", mE);
return 0;
}