(2007.1.19)がーん,新聞の答えは4だ。何故ー?と思って問題を読み直してみると,「どのマスも一度だけ通って」とある。「一度だけ」がポイントだったのね。ショック…
10回くらい読み直してようやく気づいた。
応募数179で正解率11%。私と同じミスをした人が沢山いたと思われる。
プログラムを書き換える気力も湧かないので,これ以降の記述は全て間違い。
プログラムの実行結果は以下の通り。
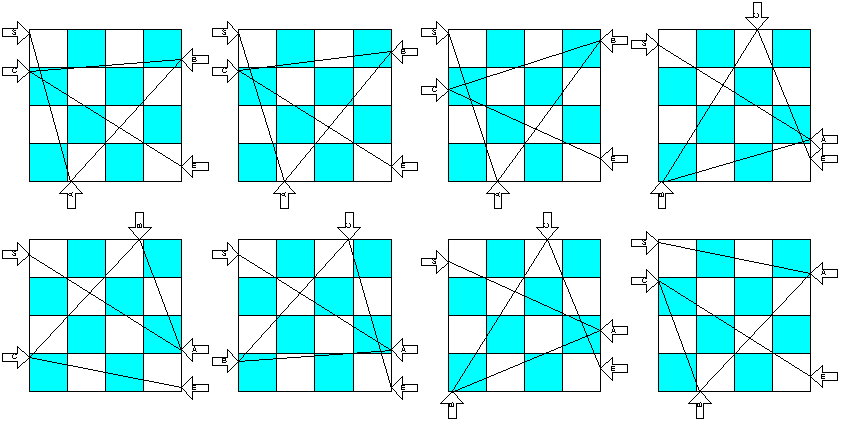
Find 1113 8c46 e300 3e8 S 0 39 A 11 0 B 40 32 C 0 29 E 40 4 Find 1113 8c46 f100 3e8 S 0 39 A 12 0 B 40 34 C 0 29 E 40 4 Find 1113 8c46 e300 1f8 S 0 39 A 13 0 B 40 37 C 0 24 E 40 6 Find 17c0 8f 6231 c888 S 0 36 A 40 11 B 1 0 C 26 40 E 40 6 Find 17c0 c880 6231 f S 0 36 A 40 11 B 29 40 C 0 9 E 40 1 Find 17c0 c7 6231 c888 S 0 36 A 40 11 B 0 8 C 29 40 E 40 1 Find 1f80 c7 6231 c888 S 0 34 A 40 16 B 1 0 C 26 40 E 40 6 Find f000 8c46 113 3e8 S 0 39 A 40 31 B 11 0 C 0 29 E 40 4 8 件発見, 1129.61 秒(約18分)
これを図にしてみると以下のようになる。見た目,線が矩形の頂点を通過しているように見えるが拡大すると微妙にずれているのが判る。

今回作成したプログラムでは矩形との重なり方が同じ場合重複チェックで単純にはじいていたが,頂点との距離も考慮し,より長いものが出現したときそちらを採用する仕組みを用意すればもう少し絵が判りやすくなっただろう。
プログラムのソースは以下の通り。
#include "puzutl.h"
const ulong bit0 = 0x00000001; // 16個の矩形と直線との交わりを表現する
const int N = 10; // 一つの矩形の点の数
const int N4 = 4*N; // 一辺にある調査点の数
const int Nrect = 4*N4; // 4辺全てにある調査点の数
struct Point {
int x;
int y;
};
int operator==( const Point& p1, const Point& p2) // 点が同じ位置にあるか?
{
return p1.x == p2.x && p1.y == p2.y;
}
Point Q[Nrect+10/*予備*/]; // 外壁上の全ての調査点
void set_point( Point& p, int ix, int iy) // Pointに(ix,iy)を設定する
{
p.x = ix;
p.y = iy;
}
void get_rect_point( int irect, Point& lb, Point& lt, Point& rb, Point& rt)
// 16個の小矩形の4点の座標位置を求める。
{
assert( irect >= 0 && irect < 16);
// +--+--+--+--+
// |12|13|14|15|
// +--+--+--+--+
// | 8| 9|10|11|
// +--+--+--+--+
// | 4| 5| 6| 7|
// +--+--+--+--+
// | 0| 1| 2| 3|
// +--+--+--+--+
// ↑Y →X
int ix = ( irect % 4 ) * N;
int iy = ( irect / 4 ) * N;
set_point( lb, ix+0, iy+0);
set_point( lt, ix+0, iy+N);
set_point( rb, ix+N, iy+0);
set_point( rt, ix+N, iy+N);
}
int get_point_line_relation( const Point& p, const Point& p1, const Point& p2)
{
// 直線 p1-p2 と 点 p の位置関係を返す。
// p1-p2 と p1-p の外積を求めることで解決する。
int ax = p2.x - p1.x;
int ay = p2.y - p1.y;
int bx = p.x - p1.x;
int by = p.y - p1.y;
int vp = ax*by - ay*bx;
return vp;
}
int min4( int a, int b, int c, int d) // a,b,c,dの最小値
{
return min( min(a,b), min(c,d));
}
int max4( int a, int b, int c, int d) // a,b,c,dの最大値
{
return max( max(a,b), max(c,d));
}
void dump( cstring msg, const Point& p) // 座標位置をメッセージと共に出力する
{
ps( "%s %d %d\n", msg, p.x, p.y);
}
YesNo is_cross_rect_line( const Point& lb, const Point& lt, const Point& rb, const Point& rt, const Point& p1, const Point& p2)
{
// 以下の矩形と直線p1-p2 が交わるか?
// lt---rt
// | |
// lb---rb
int flg_lb = get_point_line_relation( lb, p1, p2); // >0 or 0 or <0 で返る
int flg_lt = get_point_line_relation( lt, p1, p2);
int flg_rb = get_point_line_relation( rb, p1, p2);
int flg_rt = get_point_line_relation( rt, p1, p2);
if( flg_lb == 0 || flg_lt == 0 || flg_rb == 0 || flg_rt == 0) return 0; // この問題では矩形の頂点が直線上にあるときは解にならないので
// 符号が全て同じならば交わらない。
// 一つでも違う符号があれば交わる。
int min_flg = min4( flg_lb, flg_lt, flg_rb, flg_rt);
int max_flg = max4( flg_lb, flg_lt, flg_rb, flg_rt);
if( min_flg > 0) return NO; // 交わらない
if( max_flg < 0) return NO; // 交わらない
return YES; // 交わらない場合を除去したので交わるはず
}
int get_cross( const Point& p1, const Point& p2) // 直線と16個の矩形が交わるかどうか調べる
{
// +--+--+--+--+
// |12|13|14|15|
// +--+--+--+--+
// | 8| 9|10|11|
// +--+--+--+--+
// | 4| 5| 6| 7|
// +--+--+--+--+
// | 0| 1| 2| 3|
// +--+--+--+--+
// 16個の矩形と直線p1-p2 と交わる矩形を求める。
// 結果は矩形を示すビットで返す。
int bits = 0;
for( int i=0; i< 16; i++) { // 16個の矩形を調べる
// 矩形の4つの点を求める
Point lb, lt, rb, rt;
get_rect_point( i, lb, lt, rb, rt);
if( is_cross_rect_line( lb, lt, rb, rt, p1, p2)) { // 矩形と直線が交わるか?
bits |= bit0 << i; // 交わる場合その矩形を示すビットをONにする
}
}
return bits; // !=0 の場合交わる
}
void make_Q( int& nQ, int& ix, int& iy, int dx, int dy) // 外壁の初期データを作成するために使う
{
for( int i=0; i< N4; i++) {
ix += dx;
iy += dy;
nQ++;
Q[nQ].x = ix;
Q[nQ].y = iy;
}
}
int main( int argc, cstring argv[])
{
ProcTime pt;pt.start(); // 実行時間が結構かかるので調査する
Point A, B, C, S, E; // S → A → B → C → E の順に進む
// 外壁上の調査点 Q[]を作成しておく。
int nQ = 0;
int ix = 0, iy = 0;
make_Q( nQ, ix, iy, +1, +0); // 下辺
make_Q( nQ, ix, iy, +0, +1); // 右辺
make_Q( nQ, ix, iy, -1, +0); // 上辺
make_Q( nQ, ix, iy, +0, -1); // 左辺
assert( nQ == Nrect);
int idx_no_wall_S_low = N4+N4+N4, idx_no_wall_S_high = idx_no_wall_S_low + N; // 壁がない場所(入口)
int idx_no_wall_E_low = N4 , idx_no_wall_E_high = idx_no_wall_E_low + N; // 壁がない場所(出口)
set<string> finded; // S,Eが違うけど16個の矩形との重なり方が同じ場合を検出するため
int num_find = 0;
for( int a=0; a< 3*N4; a++) {
if( a % N == 0) continue; // 矩形上の点は問題外
if( a >= idx_no_wall_S_low && a <= idx_no_wall_S_high) continue; // 壁がない場所(入口)では跳ね返り出来ない
if( a >= idx_no_wall_E_low && a <= idx_no_wall_E_high) continue; // 壁がない場所(出口)では跳ね返り出来ない
A = Q[a];
for( int b=0; b< Nrect; b++) {
if( b % N == 0) continue; // 矩形上の点は問題外
if( b >= idx_no_wall_S_low && b <= idx_no_wall_S_high) continue; // 壁がない場所(入口)では跳ね返り出来ない
if( b >= idx_no_wall_E_low && b <= idx_no_wall_E_high) continue; // 壁がない場所(出口)では跳ね返り出来ない
B = Q[b];
if( A == B) continue; // 同じ点は調べない
for( int c=0; c< Nrect; c++) {
if( c % N == 0) continue; // 矩形上の点は問題外
if( c >= N && c < N+N) continue; // Cは出口と同じ外壁上には無い
if( c >= idx_no_wall_S_low && c <= idx_no_wall_S_high) continue; // 壁がない場所(入口)では跳ね返り出来ない
//if( c >= idx_no_wall_E_low && c <= idx_no_wall_E_high) continue; // 壁がない場所(出口)では跳ね返り出来ない
C = Q[c];
if( C == A || C == B) continue; // 同じ点は調べない
for( int s=1; s< N-1; s++) {
S = Q[3*N4+s];
if( S == A || S == B || S == C) continue; // 同じ点は調べない
for( int e=1; e< N-1; e++) {
E = Q[N4+e];
if( E == A || E == B || E == C || E == S) continue; // 同じ点は調べない
// SA, AB, BC, CE と 矩形の関係を求める。
int crossSA = get_cross( S, A); // 16個の矩形と直線SAが交わるか?
int crossAB = get_cross( A, B); // 16個の矩形と直線ABが交わるか?
int crossBC = get_cross( B, C); // 16個の矩形と直線BCが交わるか?
int crossCE = get_cross( C, E); // 16個の矩形と直線CEが交わるか?
int cross = crossSA | crossAB | crossBC | crossCE;
if( cross == 0xFFFF) { // 16個の矩形全てと交わる?
char buf[128];
sprintf( buf, "%x%x%x%x", crossSA, crossAB, crossBC, crossCE); // 矩形と直線SA,AB,BC,CEの交わり方
if( finded.find(buf) == finded.end()) { // 過去に同じ交わり方が見つかっていないときだけ出力する
ps( "Find %x %x %x %x\n", crossSA, crossAB, crossBC, crossCE);
dump( "S", S);
dump( "A", A);
dump( "B", B);
dump( "C", C);
dump( "E", E);
finded.insert( buf);
num_find++;
}
}
}
}
}
}
}
pt.end();
ps( "%d 件発見, %g 秒(約%d分)\n", num_find, pt.sec(), (int)(pt.sec()/60));
return 0;
}