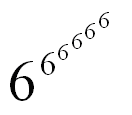 の下3桁を求める。
の下3桁を求める。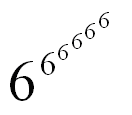 の下3桁を求める。
の下3桁を求める。
苦手なタイプの問題だ。
下3桁を求めるだけで良いので,計算も下3桁だけを行えば良い。
まともに計算すると爆発する。
下3桁だけなので,1000回以内に循環する部分が必ず出現するはず。
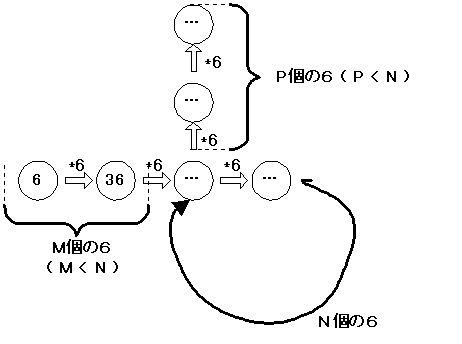
まず循環する部分を見つける。
//--------------------------------------------------------------------
// 6x6x6x… の循環を見つける。
//--------------------------------------------------------------------
int num = 6; // 初期値
int loop[1000+1] = {0};
for( int i=1; i< 1000; i++) {
num *= 6;
num %= 1000; // 下三桁だけを調べて循環を探す
if( loop[num]) { // 循環発見
M = loop[num];
N = i-loop[num];
break;
}
loop[num] = i; // 循環発見用に印を付ける
}
あとは循環を使って掛け算をさぼる関数を作成する。
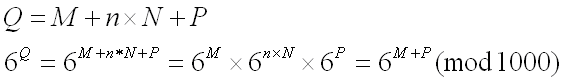
であるから冪乗を計算する毎に循環部分をさぼるような関数を作成して完了(2006.11.6 勘違いをしていた)。
int pow6( int n) // 6**n
{
int s = 6;
for( int i=1; i< n; i++) {
s *= 6;
s %= 1000; // OverFlowを避けるため下3桁のみ
}
s %= N; // 循環をさぼる
return s;
}
int p = pow6( pow6( pow6( pow6( pow6( 6)))));
int x = pow3( 6, p); // 下3桁のみの6**p
ps( "%d\n", x);
答えは1件出力されました(当たり前)。
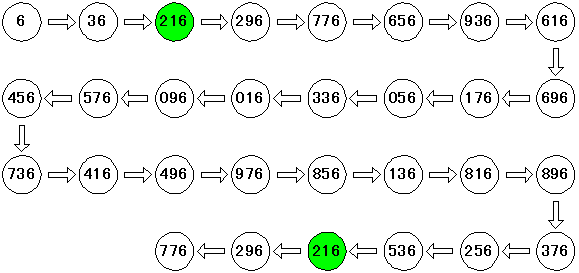
実際の下3桁の掛け算は以下のようになる。
最近果物をジュースにして飲むことが多いんだけど,市販の100%ジュースとは味が違う。
やはり搾りたてのがおいしい。
解速度
即