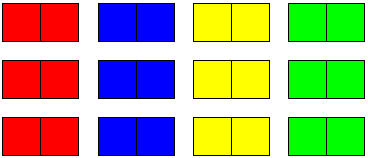
赤,青,黄,緑の1x2の大きさのブロックが,それぞれ3個ずつ合計12個ある。

これを5x5の矩形に重ならないように配置する。縦,横どの列を見ても同じ色のブロックが2個以上無いように配置するにはどうすれば良いか?

ブロックを縦置き,横置きの2通り考えると5x5の矩形に約25x2=50通り(実際は40通り)の置き方がある。
同じ色のブロックが3個あるから,それを配置する場合の数は約40x40x40(64,000)通り。
虱潰すことを考えると4色あるので,64,0004(16777216000000000000)通り。
実用的でないので,仕様に沿った制約を組む。
同じ色のブロックを矩形に配置するとき,40x40x40でなく,同じ色のブロックが同一列上に2個以上無いようにする。
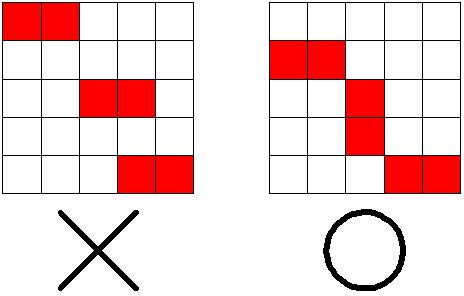
例えば上図で×の配置は出来ない。
この絞り込み部分のプログラムは以下のようになる。
// まず,5x5の矩形にビットを割り当てる。
int bits[5][5];
for( row=0; row< 5; row++) {
for( col=0; col< 5; col++) {
bits[row][col] = bit;
bit<<=1;
}
}
// ブロックをビットで表現する。
// ブロックの置き方は,25カ所に縦,横の2通りの置き方があるので,高々25x2通り=50通り。
int color[50]; // 高々50通りの置き方がある
int ncolor = 0;
for( row=0; row< 5; row++) {
for( col=0; col< 5; col++) {
if( exist(row+0,col+1)) { // 横置き
color[ncolor++] = bits[row][col] | bits[row+0][col+1];
}
if( exist(row+1,col+0)) { // 縦置き
color[ncolor++] = bits[row][col] | bits[row+1][col+0];
}
}
}
// 全部でncolor通りの置き方があった。
// 今度は,ncolor通りの置き方を3つ組み合わせた置き方がいくつあるか調べる。
// 同じ色のブロックが3個あるので。最大ncolor*ncolor*ncolor通りの置き方がある。
int* pattern = new int[ncolor*ncolor*ncolor];
int npattern = 0; // 実際に何通りの置き方があるか。
for( i=0; i< ncolor; i++) {
for( j=i+1; j< ncolor; j++) {
for( k=j+1; k< ncolor; k++) {
if( (color[i] & color[j]) ||
(color[j] & color[k]) ||
(color[i] & color[k])) {
// ブロック同士が重なっている。同じ位置に置けない
continue;
}
// 同じ行,列に置けない。
if( samerc( color[i], color[j], color[k])) continue;
// 5x5の矩形に同じ色の3個のブロックを置けた。
pattern[npattern] = color[i] | color[j] | color[k];
npattern++;
}
}
}
実際に求めてみるとnpatternが144になる。ここから先は虱潰しても大したことは無い。
// ブロック3個を5x5に置く場合の数は全部でnpatternある。
int colorA, colorAB, colorABC, colorABCD;
int a,b,c,d;
// この組み合わせで互いに重ならないように置けるか調べる。
for( a=0; a< npattern; a++) {
colorA = pattern[a];
for( b=a+1; b< npattern; b++) {
if( colorA & pattern[b]) continue;
colorAB = colorA | pattern[b];
for( c=b+1; c< npattern; c++) {
if( colorAB & pattern[c]) continue;
colorABC = colorAB | pattern[c];
for( d=c+1; d< npattern; d++) {
if( colorABC & pattern[d]) continue;
colorABCD = colorABC | pattern[d];
// Find
}
}
}
}
結果,2件が出力されました。向きが違うだけなので実質1件。
木曜夜中にフジテレビで「コマネチ大学数学科」という番組をやっている。結構面白いと思う。
解速度
即