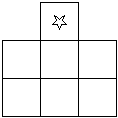
以下のような7枚の正方形を組み合わせた凸図形を2つのパーツに分割し☆部分に別々の正方形が3つ来るような分割を考える。パーツを裏返すのはダメ。
新聞の問題を良く理解せずに考えた最初の答え(最初新聞の問題文が良く理解できなかった)。
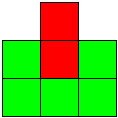
これだと，Ａ，Ｂの正方形が☆の位置に来るけどこれ以外は無いから，2つの正方形だけになる。
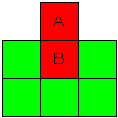
新聞の問題をもう一度読み直す。正方形が３つとある。ダメじゃん。
ならば以下のような図形でどう？120度ずつ回転すれば同じ図形になるので正方形が３つ。これで良し。
<=
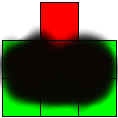(1時20分:なんかこれが正解のような気がしてきたのでここに書いた図形は一応墨塗りということにします)
しかし，問題をよく読むと，「3つの別々の正方形を持ってこられるようにします」とある。この問題文の意味するところは「最初の凸図形を構成する7枚の正方形のうちの3枚」という意味だよね。
だから多分これじゃダメ。問題のレベルも難だしこれじゃ簡単すぎる。ただ，他の答えが見つからないんだよね。
うーん，判らん！お手上げだー。
気になるのは問題文にある「そのようにできるパーツの例をあげてください」である。実は上の図形は赤と緑の境界にまだ余裕があるから，赤の■を全体が相似になるように引き延ばすことが出来るんだよねー。
(1時20分)実際の問題は凸型でなくて，それを逆さまにした図形になっている。何故凸でないのか理由を考えたらやはり上に書いた図形が正解のような気がしてきた。何処かの企業のロゴになってしまうのではないか?そういう意味もあって敢えて逆さまにしたんじゃないのかな?
今回は問題文の解釈が難しいので問題そのものを載せておく。「3つの別々の正方形を持ってこられるようにします」って所をどう解釈します?最初に「正方形7個からなる図形」って断っているから，その7個の中から3つを持ってくると解釈するのは間違っていないとは思うんだけどなー。「パーツは図の点線にそって切り分けるとは限りません」は私は「3個の正方形以外の場所」って解釈しました。でも多分上に書いた図形が正解になるのでしょう。
