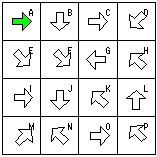
以下のように4x4の矩形内に矢印がある。矢印の方向に進み全てのマスを一度ずつ訪ね出発点に戻る経路を求める。出発点は左上のマスとする。

今日は非常に強力な台風が関東地方を直撃予定。外出しないようになんてテレビで言っている。パズルパーク応募者激増か?
A,B,C,Dのマスに注目すると,(C,D)の組合せで通過しなければならず,Cを通過するのはHを通過する場合に限ることが判る。
更にHを通過するためにはLを通過しなければならない。
Lを通過するにはIを通過しなければならない。
Iを通過するにはNを通過しなければならない。
以下の順は確定する。
N ⇒ I ⇒ L ⇒ H ⇒ C ⇒ D
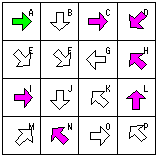
Nを通過するにはBかJを通過しなければならない。ここで始めて候補値が2つ出てきた。ひとまず保留。
Mを通過するにはDを通過しなければならない。
Oを通過するとPを通過する。
Oを通過するにはEを通過しなければならない。
Eを通過するにはGを通過しなければならない。
以下の順が確定する。
G ⇒ E ⇒ O ⇒ P
D ⇒ M
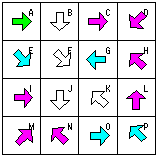
ここまで来ると後はグレー部分(G,M)を連結し,残った白地を何とかするだけ。
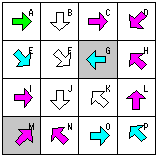
前回に続き今回も簡単に頭だけで解けてしまった。
マズイなー,こういう問題はプログラムを作って解きたかった。
ということで,一応プログラムも作ってみた。基本的な探索問題である。
今いる位置を緑色のマスとする。進む方向に番号を付ける。
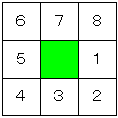
こうすると問題は以下のような2次元の配列で定義できる。
int P[4][4] = { // 進むべき方向を示す,1:東,2:東南東,3:南,4:南南西,...
{ 1, 3, 1, 4},
{ 2, 2, 5, 6},
{ 1, 3, 6, 7},
{ 8, 6, 1, 6},
};
探索関数は以下のように再帰的に定義できる。levelは再帰の深さになる。
void find( int level, int row, int col)
{
[row,col]の組合せが有効な位置か?
Goalか?
訪問済みか?
[row,col]を訪問済みにする。
P[row][col]によって次に進むべき方向が判る。
進行方向にある全てのマスで find(level+1) する。
[row,col]の訪問済みフラグを取り消す。
}
訪問済みかどうかは2次元配列で以下のように定義する。levelを記録し,訪問順序が判るようにする。
int once[4][4]; // 訪問順を記録する,訪問済みかどうかの判定にも利用する
進行方向にある全てのマスで find() するコードは以下のようにする。
int tmprow = row, tmpcol = col, drow, dcol;
switch( P[row][col]) { // 次に進む方向を決める
case 1:drow = 0; dcol = 1; break;
case 2:drow = 1; dcol = 1; break;
case 3:drow = 1; dcol = 0; break;
case 4:drow = 1; dcol =-1; break;
case 5:drow = 0; dcol =-1; break;
case 6:drow =-1; dcol =-1; break;
case 7:drow =-1; dcol = 0; break;
case 8:drow =-1; dcol = 1; break;
default:
pe( "Program Error\n");exit(16);
}
tmprow += drow; // 次の訪問位置
tmpcol += dcol;
while( exist(tmprow,tmpcol)) { // 次の訪問位置が存在するか?
find( level+1, tmprow, tmpcol); // その位置を試してみる
tmprow += drow;
tmpcol += dcol;
}
ゴールかどうかの判定は全てのマスを訪問したかどうかonce[ ][ ]を調べるのでなく,levelを調べることで簡単に判る。
if( row == 0 && col == 0 && level == 17) { goal(); return;} // level+1しながら全ての点を通過してきた?
最初の探索関数の呼び出しは
find( 1/*level*/, 0/*row*/, 0/*col*/);
答えは1つのみ出力された。
解速度
即